A Question of Rocks
I recently had the need to look into rock slides for the opening of Miranda Chase #4, Ghostrider. As usual, two simple lines led to a whole field of learning.
“He remained conscious for the next two hundred feet of descent as a [xxx thousand tons of rock swept him toward the valley floor."…"At the base of the scree slope, the mountain built a [xxx-foot high burial mound.”
Left brackets “[“ are how I note something in my manuscript that I need to look up later but don’t want to stop the flow of writing to do right at that moment. There are other facts that I do have to stop and look up because the answer will affect which direction I take the story. The volume of rock is one of the former kind. But now it was time to unearth the answers.
Weighing Rock
First, how much does rock weigh?
As part of my senior geophysics thesis in college, I had to weigh core sample that we’d drilled out in my field area. Different types of rock have different weights. Think of talc, which is a rock before it’s ground up into a powder, versus a piece of basalt or granite you tossed out of your garden. If you’ve done construction, think of the weight of a sheet of gypsum (another rock) versus a sheet of slate. I can pick up a 4’x8’x1/2” piece of “sheet rock” fairly easily. In my younger days I’d carry them in pairs. I can move a 2’x4’x1/2” piece of slate, if I’m careful and flip it end for end as I go. In my younger days, I may have been stupid enough to lift it, stupid being the operative word.
So, why was I weighing rock? Well, more dense rock also creates a strong gravitational pull. More matter equals more gravity—so denser rock formations under the ground pull down harder. I had the use of a tool called a gravimeter that could measure those minute differences. First I performed a very accurate topological survey. Then a gravimetric survey over the same area. After doing a horrendous amount of math on an incredibly advanced TI-58 programmable calculator that was the envy of my classmates (1977, $125…really dating myself here), I was able to measure the actual variations in the gravimetric field (a whole other topic that I may geek out on someday). I then could computer model (using a program I had to write in BASIC) what was occurring beneath the surface.
[caption id="attachment_22991" align="aligncenter" width="164"]
 TI 58 Calculator that powered my Geophysics thesis[/caption]
TI 58 Calculator that powered my Geophysics thesis[/caption]The Weight of Rock
This is actually much simpler now, plus I required less accuracy for fiction than for geophysics… I used Google.
The very first site I hit included this wonderful information for landscapers.
https://www.hunker.com/12422226/standard-weights-for-crushed-rock-per-meter
- Solid rock = 2.5 – 3 tons/cubic meter (NerdBonus: a “ton” is 2,000 pounds, a “tonne” is 1,000 kilograms or 2,200 pounds. So we have a mixed English/metric unit here, but I’m going with it rather than converting.)
- Uniformly crushed rock = 1.6 tons/cubic meter
- Mixed crushed rock (due to possibly better packing of space) = 1.6 – 2.2 tons/cubic meter
- Sand and chips (which I don’t care about here, but was interesting) = .92 tons/cubic meter
- I was very intrigued that all of the following come in the same at 1.07 tons/cubic meter: pea gravel, 1” crushed concrete, recycled asphalt, and 2” sewer filler rock . Pit run gravel (2” or 4”) both weigh in at 1.25 tons (that funny closest-spatial-packing effect evening things out).
- Landscaping Rock, now we’re talking:
- 2”-12” rock = 1.25 tons/cubic meter
- 12-24” rock = 1.18 tons/cubic meter
How Much Rock
For that I turned to a different website:
https://www.ngi.no/eng/Services/Technical-expertise/Rock-slides
The Norwegian Geotechnical Institute knows a great deal about rock slides. With 174 dead in the last century (most within just 3 events), they have good reason to. A big rock slide in a Norwegian fjord can create town-killing tsunamis. The 2015 movie The Wave is actually a fascinating (and good) movie about this. It’s billed as “Norway’s First Disaster Movie” and earned a nice 6.7 rating on IMDB and 83% on Rotten Tomatoes.
NGI notes that there are actually three distinct categories:
- Rock fall < 100 cubic meters. This will block a road or train track very nicely.
- Rock slide = 100-10,000 cubic meters. These only occur on slopes of 50m or more, otherwise there just isn’t enough height to get that much mass moving.
- Rock flow > 10,000 cubic meters. This caused the devasting tsunamis in 1905, 1934, and 1936.
How Much Rock
1.25 tons / cubic meter
<10,000 cubic meters (I wanted an event, not a catastrophe.)
These seemed like good working numbers.
So, the first number I wanted was easy: 12,000 tons of rock.
The second was going to take some more thought. How big a mound was created by 10,000 cubic meters?
First I needed to know the natural angle of a scree slope: 32 degrees is typical in the Scottish Cairngorms: http://www.landforms.eu/cairngorms/scree.htm. Close enough for me. My final cone had to have a radius 3 times wider than it was high.
My search for “Calculating the Volume of a Cone” brought up a neat tool right away.
I fooled around with some numbers until I got this result:
[caption id="attachment_22990" align="aligncenter" width="300"]
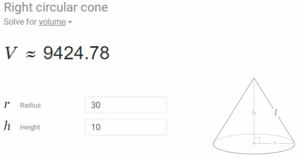 Volume of a Cone[/caption]
Volume of a Cone[/caption]Thirty meters wide and ten meters high didn’t sound very impressive as a burial mound. But then I thought about it. 1) That’s a radius of 30 meters, so a diameter of 60 meters. 2) It’s in metric.
English is always better for measurements like this. A burial mound that was 200’ across and 30’ high—way better.
But was there a better descriptor? I started tinkering.
- A circular base 200’ in diameter = 31,400 square feet.
- A football field = 47,970 square feet without the endzones. (“Covering two-thirds of a football field…” sounds a little lame.
- A FIFA soccer field is even bigger, so that wouldn’t help.
- From my on-going US Coast Guard short story series, I know that an Endurance-class cutter is 215’ long. But that’s long and narrow, so it doesn’t give the right impression.
- A US Interstate Highway uses a 12’ lane. 200’/12’ = 16 lanes. Hmmm…
But most of us don’t have much experience with picturing a 16-lane highway. I needed something familiar to most people.
- A baseball field = 400’ x 400’ = 160,000 sq feet. Nope.
- A baseball infield = 90’ x 90’ = 8,100 sq feet. Closer. Though if you start looking at specifications for the infield and the dirt running track you find out that: 1) maybe 27,000 is a workable number, but 2) there aren’t actually specific rules according to the blogs on mlb.com. So picturing something that’s variable…nah!
- A full-sized school bus is 45’ long. Hmmm…
Yeah, there it is.
UberNerd Note: Yes, I considered the fact that the mound wouldn’t be accumulating on a perfectly flat valley floor, but rather at the foot of the existing 32-degree(ish) scree slope. But I couldn’t think of how doing all that extra math would make these 2 lines in the book any more impactful—rather quite the opposite, so I left truncated cones and other calcs for a different time.
Until next time: Nerd on!



